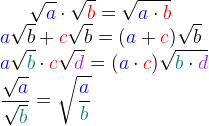
în particular,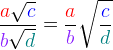
Observaţie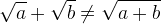
Exerciţii 1. Folosind regulile de mai sus, să se calculeze:
Operaţii cu numere reale.
Utilizarea numerelor reale în calcule presupune respectarea următoarelor reguli de calcul cu radicali: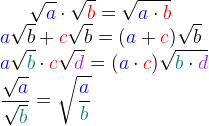
în particular,
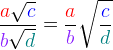
Observaţie
Exerciţii 1. Folosind regulile de mai sus, să se calculeze:
Raţionalizarea numitorului este esenţială atunci când o fracţie implicată într-un calcul nu poate fi folosită în calculele respective deoarece conţine la numitor un număr real cu radical(de exemplu, în acest caz nu am putea aduce la acelaşi numitor comun fracţia). Pentru a rezolva această situaţie, se recurge la raţionalizarea numitorului fracţiei respective, eliminând astfel radicalul de la numitor.
Raţionalizarea se face după următoarele reguli:
1. Se amplifică fracţia (atât la numărător, cât şi la numitor) cu radicalul de la numitor, ignorând orice coeficient din faţa radicalului (daca există). Aşadar, dacă numitorul este de forma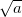
, amplificăm fracţia cu 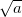. Dacă numitorul este de forma 
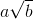, atunci amplificăm fracţia cu 
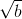. De exemplu:
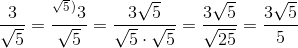
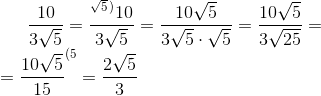
Raţionalizarea numitorului.
Raţionalizarea numitorului este esenţială atunci când o fracţie implicată într-un calcul nu poate fi folosită în calculele respective deoarece conţine la numitor un număr real cu radical(de exemplu, în acest caz nu am putea aduce la acelaşi numitor comun fracţia). Pentru a rezolva această situaţie, se recurge la raţionalizarea numitorului fracţiei respective, eliminând astfel radicalul de la numitor.
Raţionalizarea se face după următoarele reguli:
1. Se amplifică fracţia (atât la numărător, cât şi la numitor) cu radicalul de la numitor, ignorând orice coeficient din faţa radicalului (daca există). Aşadar, dacă numitorul este de forma
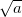, amplificăm fracţia cu 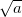. Dacă numitorul este de forma 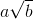, atunci amplificăm fracţia cu 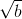. De exemplu: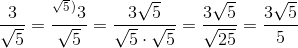
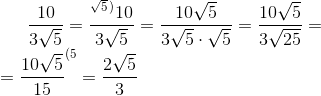
V-a fost utilă această pagină?
Nu
Da